众所周知,Splay 的复杂度分析需要用一个叫做“势能分析法”的东西。
所以首先得解释一下这个势能分析是个什么来头。
势能分析法
简介
我们在某些时间复杂度是均摊的问题上,往往进行草率的感性理解,虽然理解了复杂度是从何而来,但严谨证明却比较麻烦。
我们可以考虑在单次操作复杂度不好分析,可能复杂很大的时候(例如 splay 操作),为数据结构引入势能概念,当时间松时存储势能,当时间紧时释放势能。
可以理解为“存款”和“取款”。在某次操作耗时较少时,将盈余的时间分摊给其他耗时较长的操作。
一些定义
设一个数据结构为 D0,进行 m 次操作,分别为 c1,c2,…,cm。定义第 k 次操作后的数据结构为 Dk。定义势函数 Φ(Dk) 表示数据结构 Dk 的势能,这个函数将一个数据结构映射到一个实数上。
我们定义一次操作的摊还代价为 ci^=ci+Φ(Di)−Φ(Di−1),即本次操作的实际代价加上操作前后数据结构势能的变化量。
这样,m 次操作的总摊还代价为
i=1∑mci^=i=1∑mci+Φ(Dm)−Φ(D0)
因此,
i=1∑mci=i=1∑mci^+Φ(D0)−Φ(Dm)
这样,我们通过得出 ∑i=1mci^ 和 Φ(D0)−Φ(Dm) 的上界,就可以求出 ∑i=1mci 的上界了!
Splay 的势能分析
首先通过观察可以发现,Splay 的所有操作的代价都可以理解为常数倍的 splay 操作。
因此我们只需考虑 splay 操作。
设一个 Splay 中共 n 个点,每个点对应的子树大小为 s(i),每个点的势能 ϕ(i)=⌈log2s(i)⌉。
整个 Splay 的总势能为 Φ(D)=∑i=1nϕ(i)。
splay 操作有三种情况,下面分类讨论。
zig (zag)
当 x 的父节点为根时,我们通过一次单旋将 x 旋转到根。
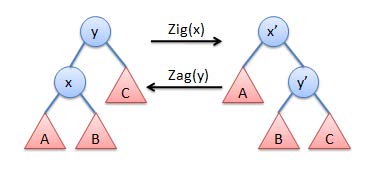
ΔΦ=ϕ(x′)+ϕ(y′)−ϕ(x)−ϕ(y)
∵ϕ(x′)=ϕ(y)
∴ΔΦ=ϕ(y′)−ϕ(x)
∵ϕ(x′)≥ϕ(y′)
∴ΔΦ=ϕ(y′)−ϕ(x)≤ϕ(x′)−ϕ(x)
因为 zig 操作需要 rotate 一次,rotate 是 O(1) 的,所以
c^zig=ΔΦ+1≤ϕ(x′)−ϕ(x)+1
同理可证 zag 的摊还代价,因为 zig 和 zag 是对称的。
zig-zig (zag-zag)
当 x 与父节点的儿子类型相同的时候,先旋转 x 的父节点,再旋转 x。
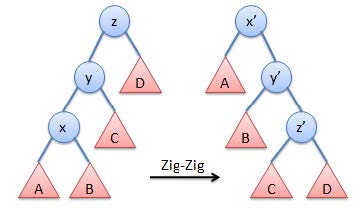
则
ΔΦ=ϕ(x′)+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)−ϕ(z)
∵ϕ(x′)=ϕ(z)
∴ΔΦ=ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)
∵ϕ(x′)≥ϕ(y′),ϕ(x)≤ϕ(y)
∴ΔΦ≤ϕ(x′)+ϕ(z′)−2ϕ(x)
我们知道,当 x,y>0,x+y≤1 时,
∵(x−y)2∴x2−2xy+y2∴x2+2xy+y2∴(x+y)2∴xylog2x+log2y≥0≥0≥4xy≥4xy≤4(x+y)2=log2xy≤log24(x+y)2
取等当且仅当 x=y。
当 x+y 取最大值 1 时,log24(x+y)2 取最大值 −2。
因此
log2x+log2y≤−2
那么,
ϕ(x)+ϕ(z′)−2ϕ(x′)=(ϕ(x)−ϕ(x′))+(ϕ(z′)−ϕ(x′))=(log2s(x)−log2s(x′))+(log2s(z′)−log2s(x′))=log2s(x′)s(x)+log2s(x′)s(z′)
∵s(x)+s(z′)≤s(x′)
∴s(x′)s(x)+s(x′)s(z′)≤1
∵s(x′)s(x)>0,s(x′)s(z′)>0
∴log2s(x′)s(x)+log2s(x′)s(z′)≤−2
∴ϕ(x)+ϕ(z′)−2ϕ(x′)≤−2
∴ΔΦ≤ϕ(x′)+ϕ(z′)−2ϕ(x)=(3ϕ(x′)−3ϕ(x))+(ϕ(x)+ϕ(z′)−2ϕ(x))≤3ϕ(x′)−3ϕ(x)−2
因为 zig-zig 操作需要 rotate 两次,所以
c^zigzig=ΔΦ+2≤3ϕ(x′)−3ϕ(x)
同理可证 zag-zag 的摊还代价,因为 zag-zag 和 zig-zig 是对称的。
zig-zag (zag-zig)
当 x 与父节点的儿子类型不同时,旋转两次 x 节点。
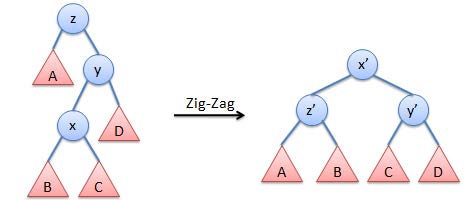
则
ΔΦ=ϕ(x′)+ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)−ϕ(z)
∵ϕ(x′)=ϕ(z)
∴ΔΦ=ϕ(y′)+ϕ(z′)−ϕ(x)−ϕ(y)
∵ϕ(x)≤ϕ(y)
∴ΔΦ≤ϕ(y′)+ϕ(z′)−2ϕ(x)=(2ϕ(x′)−2ϕ(x))+(ϕ(y′)+ϕ(z′)−2ϕ(x′))
∵s(x′)s(y′)>0,s(x′)s(z′)>0,s(y′)+s(z′)≤s(x′)
∴ϕ(y′)+ϕ(z′)−2ϕ(x′)≤−2
∴ΔΦ≤2ϕ(x′)−2ϕ(x)−2
因为 zig-zag 操作需要 rotate 两次,所以
c^zigzag=ΔΦ+2≤2ϕ(x′)−2ϕ(x)
可以再放缩一下,便于下一步计算。
∵ϕ(x′)−ϕ(x)≥0
∴c^zigzag≤3ϕ(x′)−3ϕ(x)
同理可证 zag-zig 操作的摊还代价,因为 zag-zig 和 zig-zag 是对称的。
一次 splay 操作
回顾一下,我们有:
c^zig≤ϕ(x′)−ϕ(x)+1≤3(ϕ(x′)−ϕ(x))+1c^zigzig≤3(ϕ(x′)−ϕ(x))c^zigzag≤3(ϕ(x′)−ϕ(x))
因此,我们将 x 这个点旋转到根的时候,一路抵消,最后
ci^≤3(ϕ(root)−ϕ(x))+1=3log2s(x)n+1≤3log2n+1=O(logn)
所有操作
i=1∑mci^=O(mlogn)
又因为
0≤Φ(D)≤nlog2n
所以
Φ(D0)−Φ(Dn)=O(nlogn)
因此
i=1∑nci=i=1∑nci^+Φ(D0)−Φ(Dn)=O(mlogn)+O(nlogn)=O((n+m)logn)
证毕。


