2022 年 9 月做题记录

8.29

假装已经九月了

P4822

简单的最短路。跑 $k$ 次 Bellman-Ford 即可（相当于加一维）。

本质是分层图。

P2149

建出最短路图（是一个 DAG），然后在上面找连续的重复边即可。

注意正反要分别处理。

P3807

Lucas 板子。现在终于来写了一下。

$$\binom n m \bmod p = \binom {\lfloor n / p \rfloor} {\lfloor m / p \rfloor} \cdot \binom {n \bmod p} {m \bmod p} \bmod p$$

P2700

有趣的思想（我题还是做少了，一眼没出来正解）。

考虑正难则反，改删边为加边，然后仿照 Kruskal 算法贪心从大到小尽可能加边即可。

删边连通性问题通常都可以时间倒流。

8.30

P7706

有趣的线段树。

考虑 pushup 时如何更新，观察到当前最优解一定是左儿子区间中最优解、右儿子区间中最优解、左儿子 $\max \{ A_i - B_j \}$ 与右儿子 $\max A_i$ 之和、左儿子 $\max A_i$ 与右儿子 $\max \{B_i - A_j\}$ 之和中最大的一个。

正确性：如果在“左儿子 $\max \{ A_i - B_j \}$ 与右儿子 $\max A_i$ 之和”这个情况中选出一个不合法的（$B_j$ 事实上不是最小值），那么一定会有更优合法解在“左儿子 $\max A_i$ 与右儿子 $\max \{B_i - A_j\}$ 之和” 中取到，反之亦然。

$\max \{ A_i - B_j\}$ 和 $\max \{ A_j - B_i \}$ 的更新也是类似的。

P1155

神仙题。不看题解完全不会。

观察到出现这样的模式时一个栈不能解决问题：

$$\exists i < j < k, p_k < p_i < p_j$$

这时 $i, j$ 必须不在同一个栈中。这样我们就给出了一种二分图染色的做法，如果有限制 $i, j$，则连边 $(i, j)$，然后进行二分图判定。

本题需要输出方案，因此结尾对字典序的贪心需要仔细斟酌才能过 hack 数据。。。

P4198

这道题启示我们：看似不能拼凑的东西也能间接拼凑。

具体来讲，线段树上一个区间的 ans 是由左儿子 ans 加上经左儿子影响后的右儿子 ans 时，我们想要知道左儿子对右儿子影响后的 ans 可以直接用整区间 ans 减去左儿子 ans 得到。

注意，线段树上二分的时候参数传 double。。。

CF438D

更改一个点后对这个点的有效取模操作不会超过 $\log$ 次。因此暴力取模（判一下 $\max$ 是否大于模数）即可。

AT4168

高维前缀和，维护一下某子集中的最大值和次大值即可。

P4139

扩展欧拉定理：

$$a^{b} \equiv a^{b \bmod \varphi(p) + \varphi(p)} \bmod p\ (b \ge \varphi(p))$$

按这个递归即可。递归终点 $p = 1$。

8.31

P6772

很有趣的不停优化的题。

首先非常显然的是要矩阵加速（$T \le 10^9$，图很小，边长度 $w \le 5$）。

然后先不考虑美食节，发现边长度虽然小，但是边很多，所以拆边受不了。

但是由于统计答案用的是点权（转化为到这个点之前一条边的边权），所以我们的边其实非常等价，不需要拆边，只需要拆点就行了（其实相当于共用了一下拆之后的边）。这样矩阵的规模就从 $(n + 4m) \times (n + 4m)$ 变成了 $5n \times 5n$。

然后我们发现存在美食节这个东西，显然要把每个美食节劈开处理。

然后发现劈开之后有 $200$ 段，每个内部段用矩阵快速幂，然后暴力接起来是不可接受的。

这时候我们发现我们只关心 $(1, 1)$ 的最终答案值（从 $1$ 出发回到 $1$），因此我们只需要维护一个行向量不停左乘这个矩阵，这样单次矩阵乘法的复杂度变成了 $5n^2$。

但是我们每一段依然有可能非常长，而且不能内部用矩阵快速幂了。这时我们考虑倍增地去乘这些矩阵，预处理好邻接矩阵的 $2^x$ 次方得到的矩阵，然后倍增地左乘这些东西，每段只需要乘 $\log T$ 次。

复杂度 $O((wn)^3\log T + (wn)^2k\log T)$。其中 $w$ 是边权，满足 $w \le 5$。

P2831

卡精度垃圾状压 dp 题。（为什么我必须开 long double 才能过样例？）

9.1

P1654

遇到期望 dp 时，可以考虑期望的线性性。（不要忘了！！！）

具体来讲，我们可以分开考虑每个位置对期望的贡献，然后将其加起来。

这个时候我们发现一个位置产生的贡献和当前末尾极长连续的 $1$ 的长度有关，考虑维护“到某一位置末尾极长连续 $1$ 长度”的期望。发现这里还需要其平方的期望，一块维护就好了。平方的期望不等于期望的平方！

弱化的双倍经验：CF235B

P2606

简单树上 dp 计数题。模数可能 $\le n$，所以组合数需要 lucas。

但！是！预处理阶乘逆从后往回推的时候，如果是从一个大于模数的地方往回推的话小的也会寄！

所以预处理阶乘、阶乘逆的时候必须只处理到 $\min\{n, p - 1\}$。这个很离谱，我如果没被 hack 的话想不到（因为先入为主地以为多处理一些也没问题了，但是忘记了阶乘逆是倒推回来的）。

9.4

CF222E

水了道垃圾矩阵快速幂。

9.5

P3868

用这道题复习了一下 exCRT。

就是 exCRT 板子，但是有一些坑点。

1. 可能爆 long long，需要龟速乘。
2. 可能只有一个方程，而且一开始 $b_1 = 1, a_1 \ge b_1$，直接输出 $a_1$ 会寄，需要先模上 $b_1$。

9.7

P2421

exgcd。有一点细节（主要是我脑抽了，导致调了很久）。

P6006

区间 dp 一下所有答案，动态维护一段区间的桶，不停移动即可做到 $O(n)$。

P6007

观察到本质是 DAG 上 dp，但是不需要显式地把图建出来。

转移的本质是二维数点，离线之后用树状数组处理一下就完事了。

9.8

P1450

每次询问暴力背包肯定是不行的，因此我们需要预处理一些东西。

然而我们只能预处理没有个数限制的时候（即完全背包）的方案数。

考虑容斥，用没有限制的减掉不满足限制的。观察到我们钦定一个东西不满足限制等价于将 $s$ 减去 $c_i \times (d_i + 1)$，也就是事先取出了这么多足以让它不满足限制的钱数，然后就做完了。

9.15

P6189

$O(n\sqrt n)$ 求分拆数。

法 1：五边形数定理。

考虑

$$\phi(x) = \prod_{i = 1}^{+\infty} (1 - x^i) = \sum_{i = 0}^{+\infty} (-1)^{i}x^{\frac{3k^2 \pm k}{2}}$$

再考虑到分拆数的生成函数是 $\frac{1}{\phi(x)}$。

于是可以写出分拆数的递推式

$$p_n = p_{n - 1} + p_{n - 2} - p_{n - 5} - p_{n - 7} - \cdots$$

对着这个式子递推就行。因为五边形数的增长速度是平方的，所以这个递推的复杂度是 $O(n\sqrt n)$。

法 2：根号分治 dp。

考虑分拆数的两种求法。

第一种是类似完全背包，考虑 $f_{i, j}$ 表示 $i$ 用 $1 \sim j$ 的数分拆出来的方案数，那么显然有

$$f_{i, j} = f_{i, j - 1} + f_{i - j, j}$$

第二种是考虑 $g_{i, j}$ 表示 $i$ 严格用 $j$ 个数分拆出来的方案数，那么

$$g_{i, j} = g_{i - 1, j - 1} + g_{i - j, j}$$

然后根号分治（不知道怎么想到的，在我的思维水平之上）。

我们用 $f$ 求出用 $\le \sqrt n$ 的数分拆 $n$ 的方案数，然后用 $g$ 求出用 $ > \sqrt n $ 的数分拆 $n$ 的方案数。

时间复杂度 $O(n \sqrt n)$，但是我完全不知道怎么想到这个做法的。

有点自闭。

9.16

P4053

反悔贪心。

首先显然需要按 $T_2$ 排序。

然后考虑我们想要什么。我们想知道的是在一个截止时间前最多能有多少个建筑被抢修，同时为了转移，我们还需要知道在最大化抢修建筑量的情况下，所需的最少时间是多少。

我们贪心地加任务进去，如果一个任务炸了，那么将其替换掉之前耗时最大的任务即可。可以发现这种方案一定能做到使当前解最优。

P5909

与 P4053 相同。

9.21

P6190

第一眼显然是分层图最短路，也就是暴力 dp。

但是只能拿 $90$ 分。考虑优化。

我们观察到跨过某一层的边等价于右乘一个所有边都变成负的的邻接矩阵再右乘一个最短路矩阵（应该比较显然吧）。

然后做矩阵快速幂就可以了。

9.28

P7961

垃圾 dp 题。没啥好说的。

注意：在瓶颈上的任何可以优化的地方一定要优化。这个题千万不能带 $\log$。

P7962

发现操作本质是交换差分数组。发现方差最小时差分数组一定是单谷的。

dp。考虑从小往大依次加入差分值，每次判断这个差分值是放在左边还是右边最优。

（感觉想到从小往大加入差分，也就是从中间往两边扩展着填数是关键）

朴素的做法是 $O(n^2 a)$ 的。

考虑在 $\max a_i \le n$ 的时候，一定会有一些差分值为 $0$，这些时候都没有必要去转移。

这样复杂度就是 $O(na^2)$ 的了，可以通过本题。

P7115

当时看这题十分吓人，现在感觉：就这？睡一觉基本上就想出来了绝大部分东西。

先考虑 $n = 2$ 的情况。我们将其中一列劈开，然后把另一列分成 $1$ 和 $2$ 两段分别浮在劈开后的这两列上方。然后把这两列倒置，把上面原来的“另一列”的部分堆到空列上，一个一个判断该放左边还是右边即可。

然后我们可以从 $n = 2$ 的情况推广。观察到我们想要每次将一种颜色处理完。

不妨设当前我们处理的颜色是 $1$。

根据刚刚的推理，我们可以让某一列中的所有的 $1$ 借助一个垃圾列让其全部浮在某一列上方。

那么我们只需要让所有列的 $1$ 都浮上来，然后把这堆 $1$ 塞到空列里，再把垃圾行整个消灭，$1$ 塞空列里，其他的都补到别的空位去。

让某一列的所有 $1$ 上浮需要 $1.5m$ 次操作。这个比较显然，用刚刚那个 $n = 2$ 做法的前半部分就行了。

那么这就是一个大约 $0.75n^2m$ 次操作的做法（因为 $n$ 在不断减少，有 $1/2$ 倍的常数）。

但是！但是！但是！我们的垃圾列的 $1$ 可能会散落到我们处理过的上浮 $1$ 的下方，这样就寄了！！！

因此，我们需要保证垃圾列中没有任何 $1$。这个可以牺牲一点常数轻松解决，如下图。

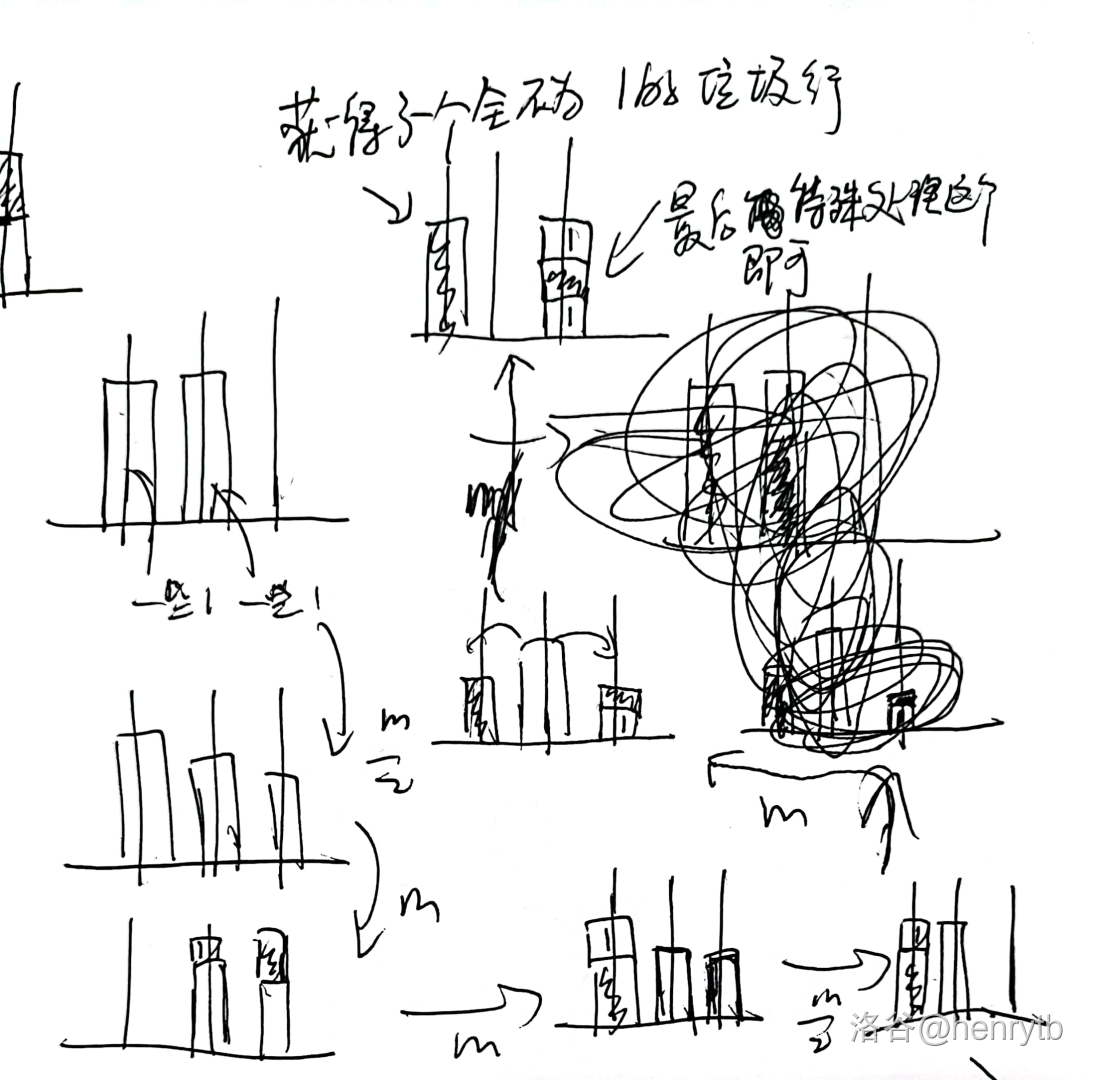
然后这题就做完了。

9.30

P1850

经典期望 dp 题。

考虑期望的线性性，转移的时候看一看每一步的期望即可。

然后发现想知道每一步的期望就得知道上一次申请没申请才能转移。于是状态就直接出来了。