一次函数的平移及对称点问题

博客真是个好东西呢，复习数学也可以在这里总结（

一次函数与图像平移

众所周知，一次函数的图像是一条直线。

以函数 $y=2x+3$ 为例：

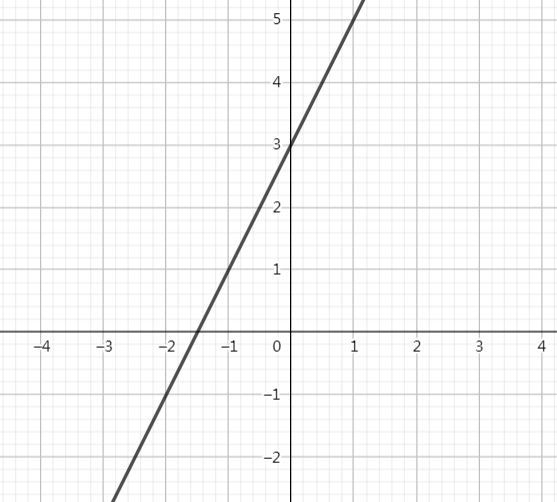
我们把它向下平移一格？

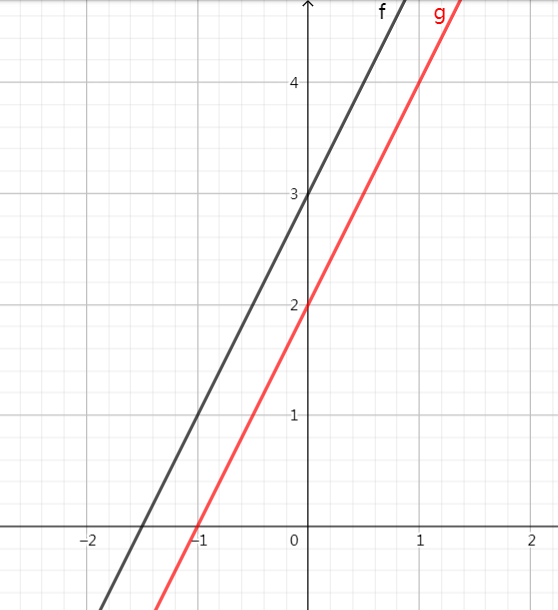
平移后的函数为 $y=2x+2$。

向上一格？$y=2x+4$。

平移 $k$ 格？$y=2x+(k+3)$

也就是说，我们得到了上下平移的规律：上加下减。

左右平移呢？

还是以 $y=2x+3$ 为例，把它向左一格？

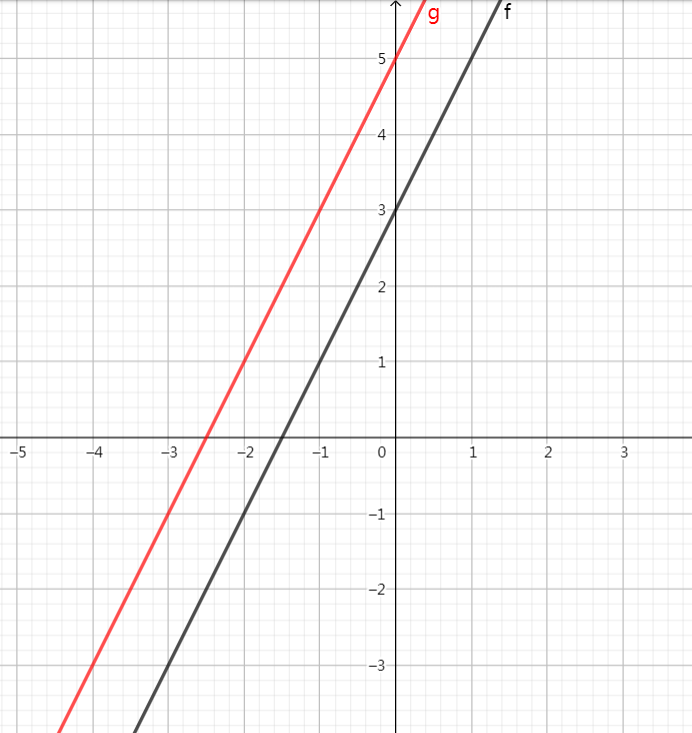
平移后的函数为 $y=2x+5$，即 $y=2(x+1)+3$。

向右一格？$y=2(x-1)+3$。

平移 $k$ 格？$y=2(x-k)+3$。

也就是说，我们得到了左右平移的规律：左加右减。

左加右减，上加下减就是一次函数平移的规律。

关于这个是为什么，我简单口胡了个解释。

因为 $y$ 是函数上一个点的 $y$ 坐标，所以往 $y$ 上面加就是往纵坐标上面加。因此上加下减。

左加右减稍微难理解一点。其实可以理解成如果要把一个直线向左平移，对于原直线上的一个点，它平移后的点肯定也向左平移了。但是平移后仅仅是向左平移，纵坐标是不变的。因此想要维持纵坐标不变，需要在横坐标上把平移的消耗给加回来。因此左加右减。

函数的图像与轴对称

我们探讨一个点关于一条直线的对称点问题。

这玩意好毒瘤啊。。

当直线与坐标轴平行时

设 $A(x_0,y_0)$，直线为 $x=a$。

则对称点 $B(2a-x_0,y_0)$。

例如：

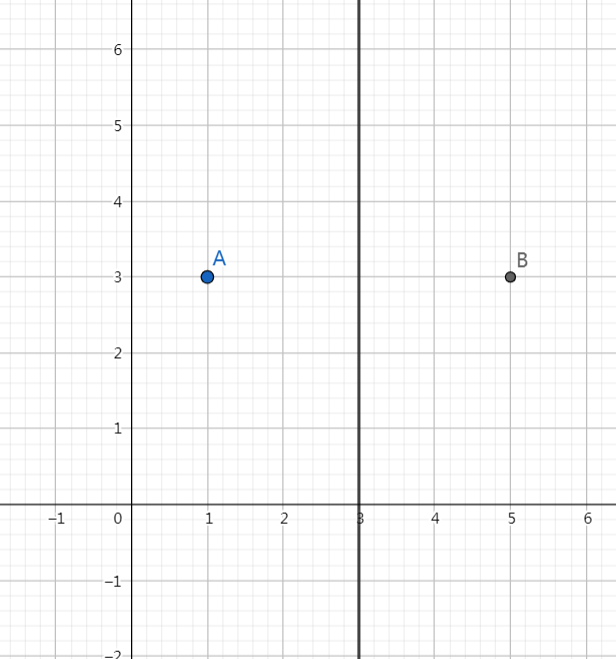
由于 $A$ 到直线的距离等于 $B$ 到直线的距离且 $AB$ 与该直线垂直，而且到直线的距离由于直线与坐标轴平行非常好求，因此我们可以快速得到 $B$ 点的坐标。

同理，当直线为 $y=b$ 时，对称点 $C(x_0,2b-y_0)$。

当直线与坐标轴成 $45°$ 角时

这个东西的结论比较特殊。

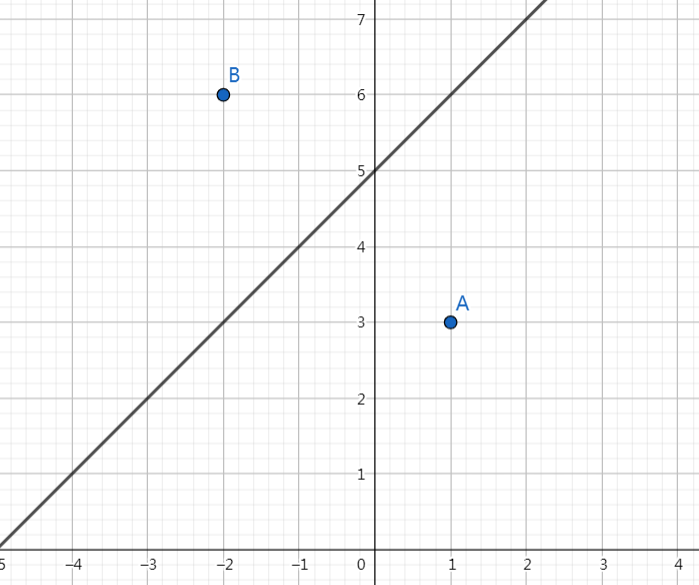
设 $A(x_0,y_0)$，直线为 $y=x+b$。

则对称点为 $B(y_0-b,x_0+b)$。

例如：

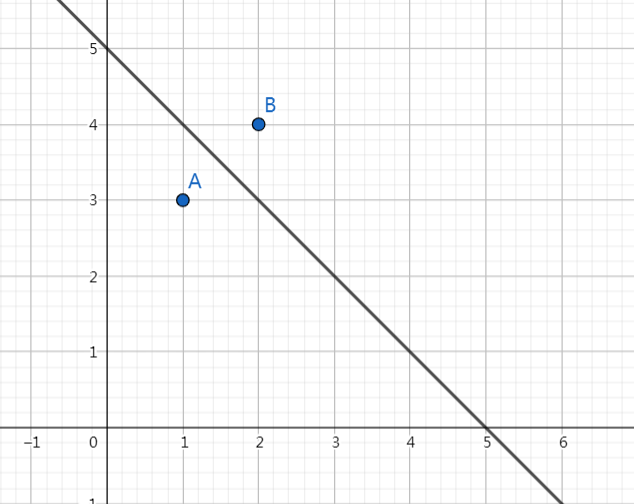
若直线为 $y=-x+b$，则对称点为 $C(-y_0+b,-x_0+b)$。

例如：

关于这两个东西的证明，我们可以自 $A$ 向该直线作一条垂线，然后倍长它就可以了。

为什么把这两个从一般情况中单拿出来呢？因为这两个东西有比较好的结论，而且有一种很好的记法。

记法：对于 $A(x_0,y_0)$ 与直线 $y=kx+b(k\in\{-1,1\})$，对称点可以写成 $B(\frac{y_0-b}{k},kx_0+b)$。

有人可能会说，这算什么好记？那么我们可以把 $x=x_0$ 与 $y=y_0$ 分别代入进去看看：

若 $x=x_0$，$y=kx+b=kx_0+b$。

若 $y=y_0$，$y_0=kx+b$，$\therefore x=\frac{y_0-b}{k}$。

分别代进去之后，求出的 $x$ 与 $y$ 刚好是该对称点的 $x,y$ 坐标！

一般情况

这个东西就不用去记了，计算方法我刚刚也说过：可以自 $A$ 向该直线作一条垂线，然后倍长它就可以了。

但是很烦人就对了…

这里给出结论：对于 $A(x_0,y_0)$ 与直线 $l:y=kx+b$，可以得出 $A$ 关于 $l$ 的对称点

$$B(\frac{(1-k^2)x_0+2ky_0-2kb}{1+k^2},\frac{2kx_0+(k^2-1)y_0+2b}{1+k^2})$$

所以我说不用去记…